In this section we explore how to factor a polynomial out of another polynomial using polynomial long division
Polynomial Long Division
The most general, intuitive, and arguably useful, type of polynomial division is polynomial long division. The key idea to learning and remembering this technique is that it is exactly the same process as you first learned for regular long division with numbers, albeit with some more complex notation and a few more potential pitfalls. It has probably been a little while since you last used long division in its most formal way though, so we will give a quick rehash here. This may seem silly, but it is extremely helpful to review the formal method of long division with numbers, so you can compare it to polynomial long division, so don’t skip this part thinking that you already know how to do long division, trust me on this! (Note: You can click the image to make it larger!)

This may seem silly, but polynomial long division works exactly like the formal version of long division. Unfortunately, the formal version of long division isn’t really the version that people tend to use, which is why the review is helpful; more as a way to make sure we are thinking about the ‘correct’ version of long division and not using mental shortcuts. People often try to do polynomial long division using the mental short-cuts they’ve developed for long division of numbers. Unfortunately that almost always goes horribly horribly wrong with polynomials.
Not to beat a dead horse, but polynomial division follows the exact same process as the formal long division above. Thus we will go through an example and point out the parallels; starting with writing out the divisor (thing we are dividing by) and dividend (the thing we are dividing) in the same spots and in the same way, and then go through the same steps (conceptually speaking).
(Note: You can click the image to make it larger!)

Non-zero Remainders
Let’s look at the example above but divide by instead of . Then we get: (Note: You can click the image to make it larger!)
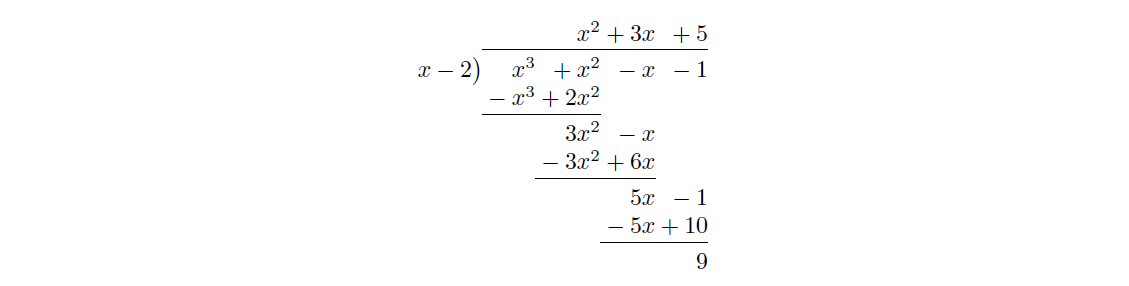
Just like with regular long division, if you have a remainder you have some choices on how to express that remainder. Let’s say you divide 45 by 7; you’d get 6 with a remainder of 3. You could proceed to find a decimal version, but sevenths tend to have terrible decimal expansion. Instead we could write it as , or we could leave it as . This is exactly what we do with polynomials. We could leave it in its original fraction form, or we could write: There is one other form that is often helpful, as we often want to replace the original polynomial with a “factored form”, rather than dividing out the divisor piece. So we can instead write: Which form we want depends on what we are doing. In either case however we can see one of the ‘factors’ is no longer a polynomial. Once that happens a lot of our tools vanish which is why we tend to only record the result of our division if it has a zero remainder; not because the long division failed (it worked just fine), but rather because the result is annoying (like dealing with the “sevenths” in our number example, rather than getting a whole number.)