Learn how to draw a torus.
Now make that ellipse smile!
Finally, add in an upside down arc:
And like magic, we have drawn a torus! On the other hand, if you want to use a computer to draw a torus, perhaps you should use the parametric formula:
where is the radius from the center of the torus to the center of the “tube,” is the radius of the “tube,” , and . However, listen, you could have derived a parametric formula using the techniques you’ve learned. Let’s do it.Use unit tangent vectors and unit normal vectors to derive a parametric
formula for a torus.
Imagine a circular curve in that runs through the donut,
shown in the diagram from the previous problem by the two “dots.” 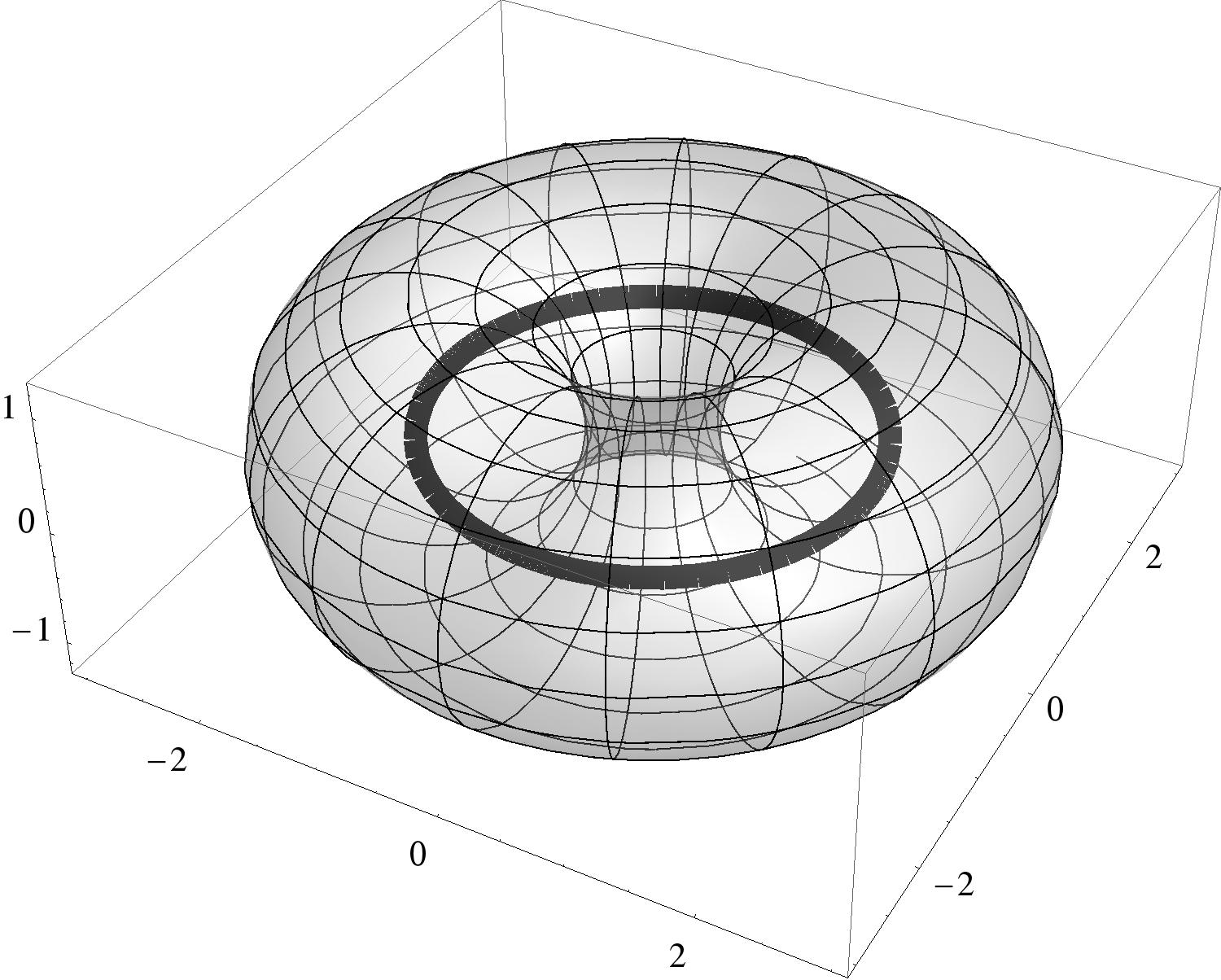 Give a formula for a vector-valued function that will draw a circle in the -plane,
centered at the origin, of radius , as runs from to . Compute , the function that will
give the unit tangent vector for any value of . Simplify your answer.
Compute , the function that will give the principal unit normal vector for
any value of . Simplify your answer. Compute , the function that will
give the unit binormal vector for any value of . Simplify your answer.
Now if we put these together we can write our torus as
Simplifying and writing the components of this formula out we see:
And done. We’ve given a parametric formula for a torus.
Give a formula for a vector-valued function that will draw a circle in the -plane,
centered at the origin, of radius , as runs from to . Compute , the function that will
give the unit tangent vector for any value of . Simplify your answer.
Compute , the function that will give the principal unit normal vector for
any value of . Simplify your answer. Compute , the function that will
give the unit binormal vector for any value of . Simplify your answer.
Now if we put these together we can write our torus as
Simplifying and writing the components of this formula out we see:
And done. We’ve given a parametric formula for a torus.

If you’re paying attention, you may notice that we now have a very similar formula
to the one given above, except that we have some minus signs where before we had
plus signs. What happened here?
We made a mistake in our work in the example
above. We lied to you when we give the initial parametric formula for the torus.
We just broke math. Everybody wins. Both formulas draw a torus.
Both formulas are correct, the first one we gave was derived using “outward”
pointing normal vectors. The second one we gave was derived using “inward”
pointing normal vectors.