This section describes one of the most useful tools in mathematics - especially in calculus - the sign chart!
Lecture Video
Text and details
In mathematics, the easiest way to divide the notion of being “past” some benchmark or not, is to consider whether the value is positive or negative. Typically this means we would arrange our function to represent the value we consider the “benchmark” as zero, and then test whether the function is positive (above the benchmark value) or negative (below the benchmark value) at whichever points we want. But, in the case where we have continuous functions there is an even easier way to do this kind of test - by breaking our domain into intervals and using the continuity to our advantage.
Let’s consider an example:
Say we have a function that tells us the profits of a company over time (in months), which is given as . We want to know which over which months the company is making a profit, and over which months the company is losing money.
To do this, we will start by finding all the zeros of the function - which times where we are exactly breaking even. To do this, we can use the zero product property - that a product of things is zero if and only if one of the factors is zero. This means that we want to know when each factor is zero, i.e. when , , or . So, solving each of these individually we get , , and .
Next we want to know where the function is continuous. This is easy to overlook, but is especially important as the sign chart is explicitly exploiting the continuity property - so it only works where the function is continuous. The easiest way to account for this, is to record any values where the function has a domain restriction. In this particular case there are no restrictions, so we don’t have to record any values for this part - this is because polynomials are continuous over all real numbers (something we will cover more later in the polynomial section).
Finally, to understand what we are about to do, recall our definition of continuity - that a function is continuous between two points if we can draw the graph between those two points without picking up our pencil. This means that, if we had a positive function value and a negative function value in some interval, then the function would have to cross the x-axis somewhere between those two values, which means it would equal zero there. But another way of saying this, is that between any two zeros, the function has to be restricted to being either entirely above the x-axis or entirely below it (this is where we are exploiting continuity, without continuity this statement isn’t true!)
So, with that in mind, we are ready to draw our sign chart!
The first step was finding all the zeros of the function, and all the domain restrictions. We did this and found that our function has no domain restrictions, and has zeros of , , and .
Step two is to draw a number-line with only the domain restrictions and zeros listed, and our function above the line on the left. In our case we have:
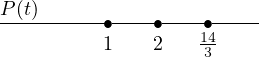
Notice that I didn’t include zero or any other “centering” value on the line, I only put the zeros of the function (and the domain restrictions, if there were any). Technically adding extra values to the line here won’t produce an incorrect result, but it will generate more work for you to do to get your answers.
Step three, we want to test values between the labeled points. To be clear, it doesn’t matter at all which value you choose to test a given interval, as long as it is strictly between the endpoints on the interval. For example, if we want to test the interval between and , we could pick , , or even . But... some of these values are obviously more of a pain to calculate than others. Indeed, since it doesn’t matter which value you choose, try to pick a value that is easy to compute with. In this case I would pick , but whatever value works for you is good.
But there is an important note here. We are not trying to actually compute the value at that point. In fact, the only thing I care about is whether the function is positive or negative at that value. So when we pick a number like to “compute” with, what I actually want to do is determine if the function is positive or negative at , not what the function actually equals. This can be a difficult thing to embrace for students, since you’ve been hammered with the “be precise and give a numeric answer” for more than a decade of schooling at this point, but not explicitly computing has advantages.
For example, if I am using , I would plug in the into the original function, getting . Actually computing this would get me to the step and multiplying out those values would be... annoying. In contrast however, I can look at each of the factors and determine if the value is positive or negative - again in our case we get that the first factor is positive, the second is negative, and the third is negative. Then, instead of multiplying the numbers, we can determine whether is positive or negative by multiplying the signs: positive times negative times negative is positive, so is positive. Again, what actually equals isn’t important for a sign chart, just whether it is positive or negative - and remembering this can save you considerable time and headaches when dealing with annoying intervals like this one.
We continue testing each interval - for the interval between and we could use . Doing this we would end up with a positive times a positive times a negative, giving that is negative between these two values.
One might think we are done, but we need to remember the left and right intervals too, meaning the interval and . The good news here, is that we can choose any value in the interval. Although you might be tempted to pick something like for the left interval or for the right interval, it’s often easier to pick some kind of absurdly large number - again the goal is to not actually compute a value at all. This is much easier if we are picking absurd numbers. For example, if we pick for the right interval, we don’t even need to actually add or subtract the or or in each factor, because those numbers are way too small to do anything to change the sign of . So we know all three factors are positive, and thus the right most interval is positive. Similarly if we choose , then each of the three factors will stay negative (since the massive negative number will overpower the values being added to it in each factor) and so, multiplying three negatives together gives that the far left interval is negative.
So, we have found that on the interval is negative, on the interval is positive, on the interval is negative, and on the interval is positive. We can represent this in the sign chart by putting a positive or negative sign above each interval, like this:
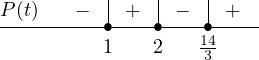
Finally, we can use this chart to answer our original question: When is the company making profit and when is the company losing money? According to our sign chart, the company is making money (positive profit) in the interval , i.e. between the end of month one and month two, which is all of February, as well as all the months past which corresponds to about two thirds of the way through the fifth month - or around May 20th, give or take. The company is losing money during the other times - specifically for all of January and between March 1st and May 20th.
It turns out, for those planning on taking calculus, the sign chart is incredibly useful in nearly all of calculus, and will show up dozens or even hundreds of times in calculus one alone for lots of different applications. As such, it is invaluable to get comfortable with building a sign chart now for those intending to move on to calculus.