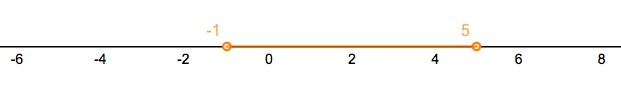Remember our facts about inequalities.
When finding the radius and open interval of convergence for Taylor series, it is
important to be comfortable working with absolute values. This assignment reviews
some of the basic properties.
I understand. I do not understand.
One of the most common mistakes that students make is that they treat the
absolute value as a linear function. In practice, this leads to mistakes like the
following:
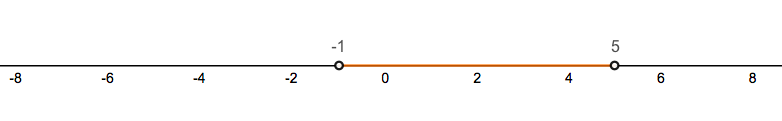

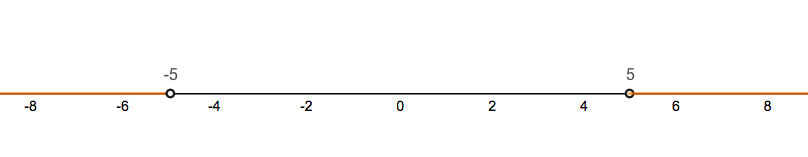
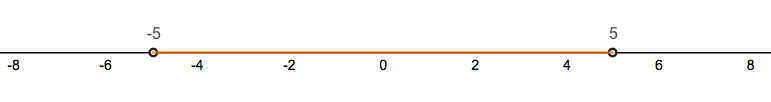
Incorrect: If then .
To see why this is incorrect, note that when , we have .
Select the interval below that correctly shows all points such that .
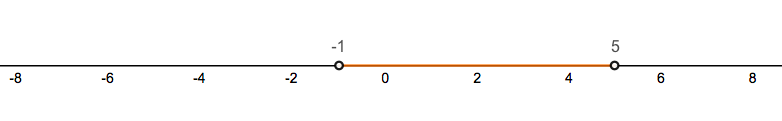

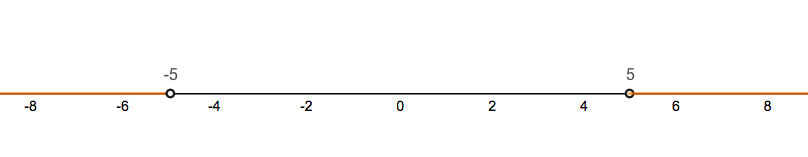
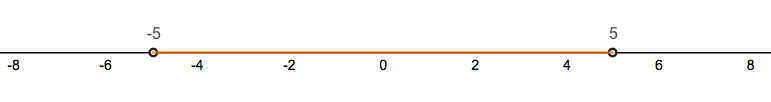
The expression can be thought of in a more geometric way as well; it represents
the collection of all points that are a distance units from a central point
.
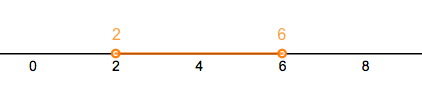 The center of this interval is at . The endpoints and are precisely a distance of 2
aways from the center . All points that satisfy the inequality are within a distance of
2 from the center.
The center of this interval is at . The endpoints and are precisely a distance of 2
aways from the center . All points that satisfy the inequality are within a distance of
2 from the center.
For example, if we consider the number line corresponding to the expression

This observation is particularly helpful when considering the interval of convergence of a Taylor series.
I understand I do not understand