We give a new method of finding extrema.
There is more than one way to solve it.
Previously, we were finding extrema of functions when constrained to some set .
Next we investigate the boundary of . To do this we must parameterize the boundary of , or express the boundary either in terms of or . In this case, we can express the boundary parametrically as or we could set or even At this point we look for critical points on the boundary. These are also candidates for the extrema. Finally if the set has “corners,” we must also consider these as candidates for the extrema.
Above we see that a crucial step in computing extrema when constrained to a set is finding an explicit formula for the boundary. This could be very difficult or even impossible! If our constraining set had been our previous method will not work, as we (at least this author!) cannot find an explicit formula describing the boundary (which in this case is the set) of the set above. Nevertheless, there is another way. It is called the method of Lagrange multipliers. This method is named after the mathematician Joesph-Louis Lagrange, which he first employed. This method relies on the gradient vector. Recall facts about the gradient vector:
- .
- points in the direction that one must leave in order to see the initial greatest increase in .
- points in the direction that is perpendicular to any level surface of .
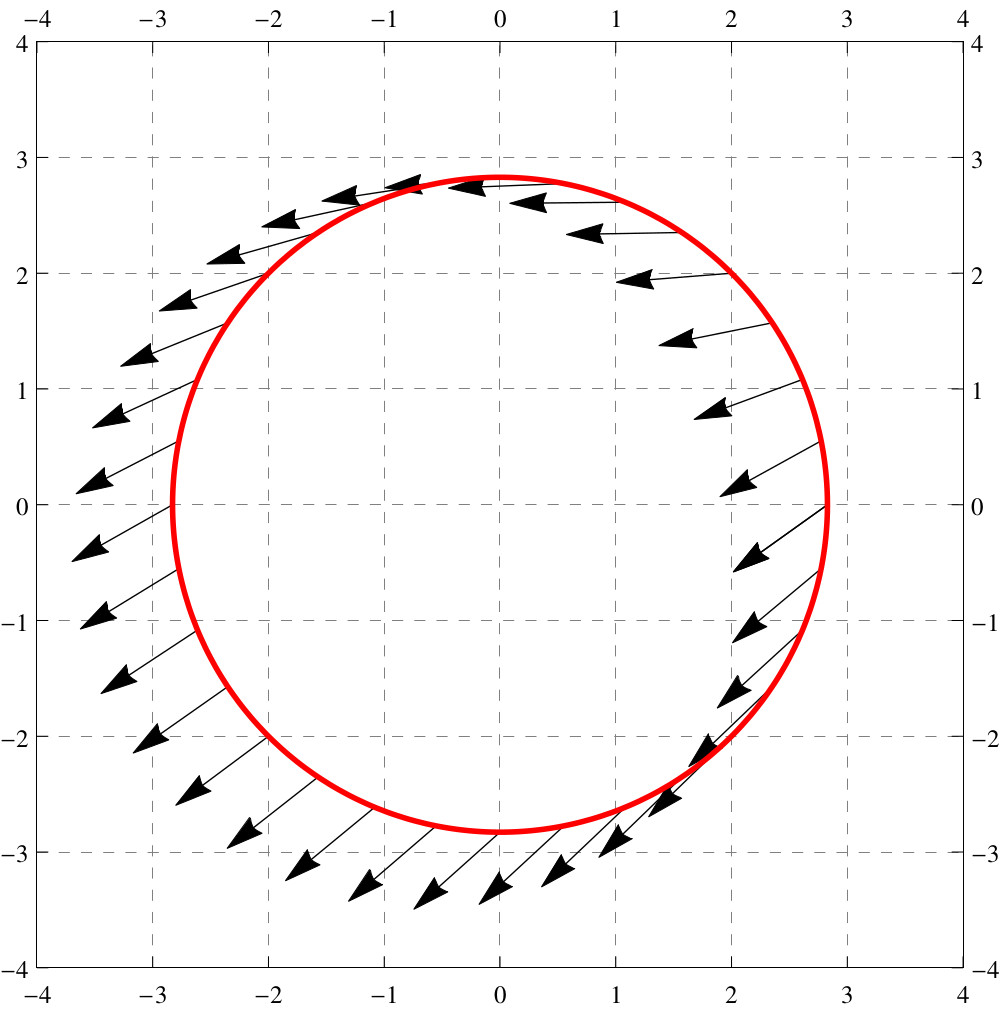
It is this last fact that we will look at now. Below we see level curves for some function along with a constraining curve that we will call :
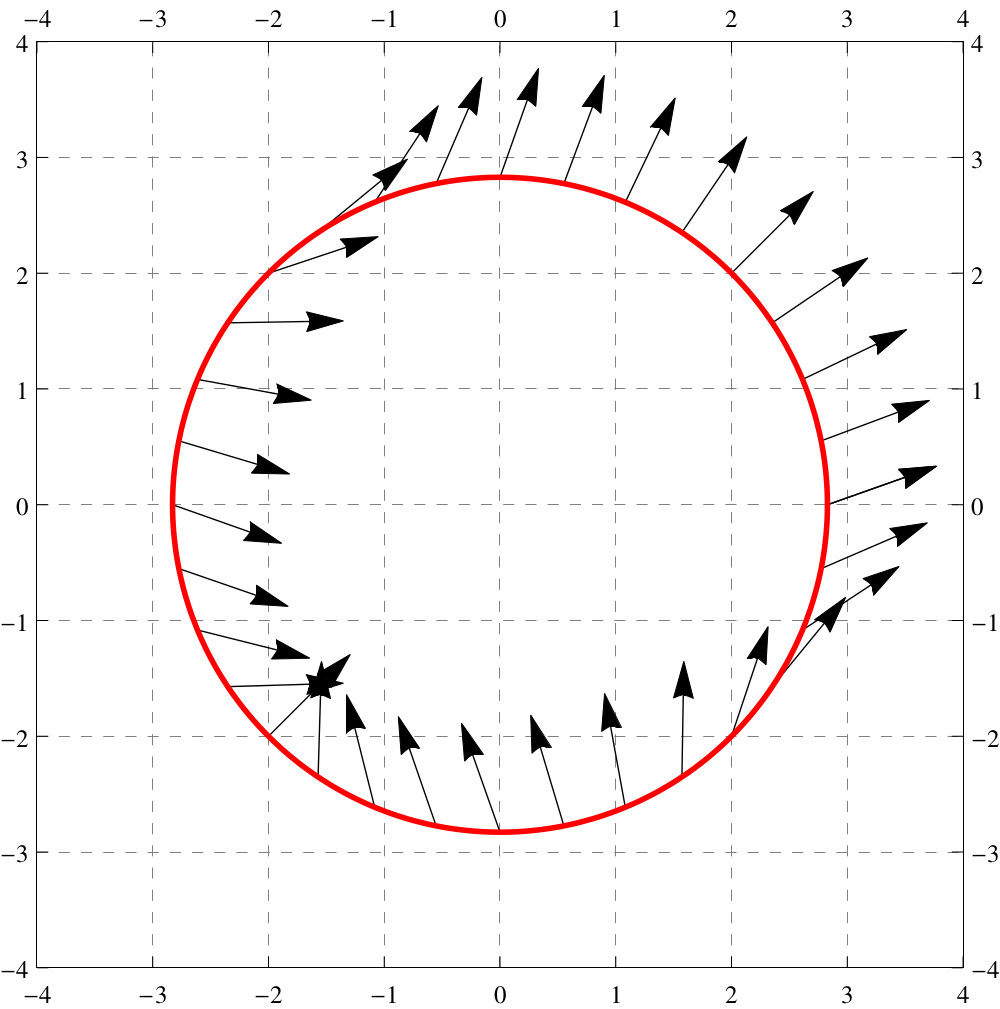
Let’s add vectors to our graph that point in the direction of . We can do this without computation, since we understand the geometry of the gradient vector, the gradient vector is perpendicular to level curves:
Now we can observe something interesting: If for some point the gradient points in the “general” direction of the tangent vectors of , then cannot give an extremal value of , as moving along will either increase or decrease the value of . Here’s the upshot:
The only candidates for local extrema occur when the gradient of is perpendicular to .
How do we find these points? To do this, we will imagine that is a level curve for some other function , and define as: now, the candidates for extrema of when constrained to a curve are found by finding such that since that satisfy this equation are those where the gradient vectors of are perpendicular to the level curve . This is the essence of the method of Lagrange multipliers.
Working with geometry
Lagrange multipliers tell us that to maximize a function along a curve defined by , we need to find where is perpendicular to . In essence we are detecting geometric behavior using the tools of calculus.
Working with algebra
Let’s work an example.
Using Lagrange multipliers, we will check all other points on by setting and computing : We need to find points such that for some number . Write with me
and Note the symmetry of the components of . From this we see that Hence Thus to find extrema for when restricted to , we check the value of at the points above. Write with me We now see, via the Extreme Value Theorem, that the absolute minimum of when restricted to is given by and the absolute maximums are at the points , , and .The Lagrangian
Finally, we should point our that there are other ways to view Lagrange multipliers.
Thus to check whether is equivalent to checking where or has undefined components. When working with constrained optimization problems by hand, the Lagrangian doesn’t help much, since your next step is to look at However, there are certain advantages to working with the Lagrangian:
- If you are working with a computer, it might be better to work in terms of the Lagrangian, as there are efficient algorithms for checking when the gradient of the function is zero.
- Working with the Lagrangian gives a method for changing “constrained” optimization to “unconstrained” optimization, as we are simply finding the critical points of .
- The Lagrangian shows us a symmetry between and .
For some interesting extra reading check out:
- Unifying a Family of Extrema Problems, W. Barnier and D. Martin, College Math Journal, November 1997.
- An “Extremely” Cautionary Tale, M. Krusemeyer, College Math Journal, March 2000.
- Lagrange Multipliers Can Fail to Determine Extrema, J. Nunemacher, College Math Journal, January 2003.
- On the Genesis of the Lagrange Multipliers, P. Bussotti, Journal of Optimization Theory and Applications, June 2003.