This section discusses how to simplify numeric and odd root-value radicals.
The Video!
The Text!
Simplifying Numeric Radicals
First we revisit a numeric factorization tool that you may (or may not) have learned quite some time ago, called a prime factor tree. This will be supremely helpful in determining the prime factors of any given number, which is necessary for simplifying a numeric radical.
We use the following steps to simplify any numeric radical: (Note: We utilize a prime factor tree to get the prime factorization of , but if you don’t remember or know what that is, we explain it in Example exTwo below, for now you can just pretend you already knew the prime factorization of .)
- 1
- Use a prime factor decomposition tree (aka a ‘prime factor tree’) to find all the prime factors.
For example, if our radicand is , we would use a prime factor tree to find the prime factors and then rewrite as .
- 2
- Write out the radicand in its prime-factor form. Optionally, you can also write the root value to make it clear.
For our example we would write .
- 3
- Rewrite each prime factor in the radicand as the product of the prime to the root value as many times as you can
(without going over) with the remainder at the end.
In our example we have . Note that you can write this instead as , or you could even write the as . The important part is to separate the “perfect squares” (since the root value is 2, i.e. we’re simplifying a “square root”) part of each prime factor from any leftover. Also note that we write the remainder explicitly to make it clear what is happening, but you could just write it as “” instead of “” if you want).
- 4
- Pull out the groups that were identified in the previous step (the “perfect squares”), leaving the remainder terms. When pulling out the groups you identified in the last step, divide each power by the root-value (this should divide evenly due to how we made the groups in the previous step) and multiply the result as a coefficient to the root.
- 5
- Finally; simplify all the resulting numbers and merge them into single values (one value for the radicand and one value for the coefficient).
As usual, this is far easier to understand by seeing an example in action. To that end, let’s see this all in action with our original example:
Simplify the numeric radical fully.
| Rewrite the radicand via prime factorization (step 1). | ||
| Separate primes into perfect squares and remainders (step 2). | ||
| Break apart radical to separate the two groups (step 3). | ||
| Evaluate the first radical (step 4). | ||
| Simplify (Step 5) | ||
Let’s consider another example; simplifying . This may seem intimidating at first, but the key here is to use the prime factor tree to decompose the large number into a product of smaller numbers. Let’s revisit how to do this before we continue.
Remember that a (prime) factor tree is a simple iterative process (meaning we just keep repeating the same step(s) until we finish). At each step, we factor the current number into any two smaller numbers. Once we find two such numbers, we draw two branches below the number, and write our factors below those branches.
For example, if our number is 100, we could use . Since we have two numbers that multiply to our value (10 and 10 multiply to 100) we write 100 down and then two lines branching down from the 100, and below each line we write 10 to show that we decomposed 100 into the two factors 10 and 10.
Then we repeat these steps on each of our new numbers. If one of the two numbers is a prime, we circle it and that ‘branch’ of the tree ends (no more factoring off that branch). Once every branch ends with a circled prime we are done factoring, and the original number is the product of all the circled numbers (which we commonly write at the top to keep track).
So, if we apply our prime factor tree method to 15120 we get: In our case we would get:
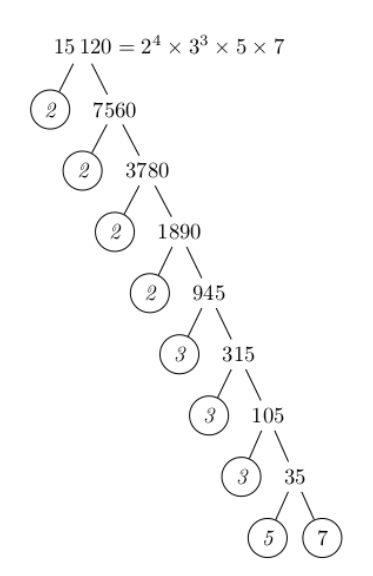
Note that it is actually faster and better if you can think of larger numbers to multiply together to get the target value. For example, with 15120, it would have been better if we saw that . This is because it would have made our tree branch out faster and more efficiently, and thus taken less effort after that step. However, that isn’t likely that you would see that 15120 is divisible by 945, and the important thing to know is that you don’t need to. Any two numbers that you see (that multiply to your target), will work - it just may take a bit longer. Eventually you will have to divide down to the same prime numbers regardless, and spending time looking for a ‘better’ number-pair to use is just wasting time instead of using a factoring you already know works.
Now that we have the prime factorization, we will write out our radical with the radicand in the factored form: As before, we want to group these terms as each factor to the root level ( in this case) with remainders. Specifically we have and , and the and are both left alone (since they have powers less than to start with). So we would write; Then, pulling out the pieces that are grouped we get: And, finally we can simplify we get:
And so we have our final simplified expression and we conclude: