This section discusses how to solve inequalities.
Video lecture
Text and Supplemental Content
To solve an inequality, we must use the algebra techniques for inequalities to isolate the independent variable. However, by their nature, inequalities usually have many solutions, rather than just one. So these solutions must also be represented as inequalities. This can be as simple as direct algebraic manipulation, but as soon as we are looking at non-linear inequalities things can get... weird.
We begin with the most basic version - a single variable linear inequality. Consider the following:
We can solve this inequality just like we would an equality, using the algebraic rules for inequalities we discussed in a previous segment.
| Starting Point | |
| Subtract 17 from both sides. | |
| Subtract from both sides. | |
And we’ve isolated the , and so we’ve got our solution to the inequality. Notice that the solution is actually an infinite set or range of numbers - it isn’t “a solution”, rather we have a “solution set”, which is “all the values strictly less than negative eighteen.”
When dealing with single variable linear inequalities, generally there isn’t much different than equalities, except you should be careful with dividing by negatives. Let’s see one more example;
| Starting Point | |
| Subtract 6 from both sides. | |
| Add from both sides. | |
| Divide by and flip the inequality. | |
Note that, when we divide by a negative (or if we multiply by a negative) we have to flip the inequality sign’s direction, but otherwise the process is pretty much the same.
Where it gets a little more interesting is when we get to non-linear inequalities. Consider the following inequality:
At first glance, this seems intractable - there doesn’t appear to be anywhere to start. But, when in doubt, try treating the inequality like an equality. If we were to instead be presented by , how would we start? We’d start by getting everything to one side and trying to factor!
| Starting Point. | |
| Move everything to one side. | |
| Factor by grouping. | |
| Factor difference of squares. | |
Now, if this were an equality, we would set each factor equal to zero and solve. But that only works for an equality, not an inequality. But, if we step back for a moment, what is that inequality actually asking? It’s asking when the product of those factors is positive. It turns out, we already have a tool for that - the sign chart!
So, we can form the sign chart for the expression , which gives us the following:
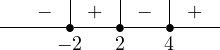
Remember that we want to know when the product is positive which, according to our sign chart, happens from and . So our solution set is .