Video Lecture

Text and Additional Details

We have an intuition of what linear approximation is trying to do, and now we will discuss the technical aspects. We will present a number of notations and vocabulary common to this subject, and introduce the variations of the formula using these different notations.

We know that linear approximation is the process of using a (nearby) easy to calculate input and a tangent line to approximate the value of a difficult to calculate input. For example, if we wanted to calculate $\sqrt {10}$ we could use the function $\sqrt {x}$ and the easy-to-compute value $x=9$, then take a derivative to get the slope of the tangent line, which allows us to find an approximation for $\sqrt {10}$. But a worthwhile question would be: can we sum up this algorithm into a single formula? Let’s motivate our analytic process with the following picture:

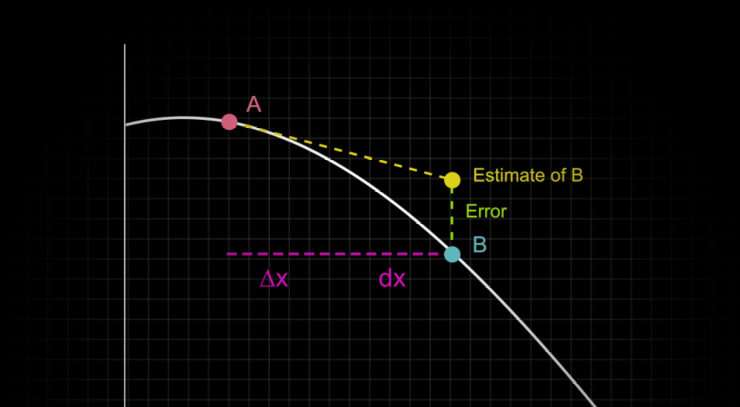
Here, point $A$ is the easy to calculate point that we use as our starting point, and $B$ is the point we want to estimate. We can see that our estimation is represented by the dashed line moving from the $x=A$ value to the $x=B$ value.

But how do we represent the process of “traveling along the tangent line”? Remember that the tangent line is (itself) a formula. So if we could find a formula for that tangent line, then we could actually plug in $x=B$ to the formula and that would give us our estimate! But we’ve already done tangent lines, so this isn’t anything new! Indeed, we know that the slope of the tangent line is just the derivative at that point (which is $f'(A)$) and the point itself (which is $(A, f(A))$). So we can use the slope-point form of a line to get our formula; $y = (f'(A))(x-A) + f(A)$. Thus, if we want to evaluate this formula at $x=B$ we get: $$\text {Estimate }= f'(A) (B-A) + f(A).$$ The key takeaway here though, is that this formula is nothing special or unique, it’s just the tangent line formula at the point $(A,f(A))$ applied specifically to the point $x=B$. In some sense, we could just as easily say that “linear approximation” is simply an application of “tangent lines”. It’s mostly because it ends up being so useful virtually everywhere in the worlds of engineering and science that it ends up with its own name.

It is worth taking a moment to see the other common way this formula is often recorded. Again I want to stress that this is more due to context, discipline, and/or notational choices of the author or instructor as to which notation is used, but they all mean the same thing.

Differential Form:

In some calculus courses or settings, this subject is taught using the idea of a “differential”. The differential is, essentially, the small change in the $x$ and/or $y$ direction that we discussed when we first introduced the idea of instantaneous rates of change. In this context, the differential represents the distance between the points $A$ and $B$, and is usually denoted by either $dx$ or $\Delta x$. So we would have the formula: $$\text {Estimate }= (f'(A))(dx) + f(A) \hspace {1cm} \text { or } \hspace {1cm} \text {Estimate }= (f'(A))(\Delta x) + f(A)$$

So we’ve seen that linear approximation, although incredibly useful in just about every area of science, is actually nothing more than the application of a tangent line to get an estimate of a difficult-to-calculate value of a function, assuming you have an easy (or easier) to compute value nearby. This formula has different common forms, but the notation and vocabulary all represent the same idea, just different contexts and discipline conventions result in different forms for this idea.