NOTE: There may be random lines that look like \texttt{(SOME TEXT)} and maybe even some { } within that text. You can ignore everything that isn’t the text itself; ie the texttt bit and the braces, they are an artifact of how some randomization is being done that I haven’t had time to fix yet. If you literally delete the \texttt and the braces from what you see, and just keep the text itself, it will read exactly as intended. So just ignore all those texttt and braces whenever you see them.

Also note: Some of the below has randomized elements, some do not. Currently Xronos does not support randomized graphing (although we’re working on it!) so a lot of the graphing problems won’t randomize, but a surprising amount of the other problems will change values or text if you hit the green “another” button in the top right corner to get another version of this practice exam. This also means it may take some time for the entire test to render because we have to rely on public servers to do the randomization for us currently, so please be patient. If it takes more than 3-5 minutes to fill out the random values (meaning: if there are still spinning wheels of death going after 3-5 minutes) there is a problem. Try hitting the “another” button to see if it resolves itself. If it keeps doing this, please contact your instructor and let him know!

Simplify the following: $\dfrac {\sage {p1CNEc5}}{\sage {p1CNEc6}}$.

Simplify the following: $\sage {p2CNEc5} + \sage {p2CNEc6}$.

Consider the polynomial: $p(x) = (\sage {p1CNMf1}) + (\sage {p1CNMf2}) + (\sage {p1CNMf3}) + (\sage {p1CNMf4}) + (\sage {p1CNMf5})$. If we know one of the roots is a non-real complex number, what is the best we can say about the number of real roots that $p(x)$ has?

Consider the polynomial: $p(x) = (\sage {p1CNMf1}) + (\sage {p1CNMf2}) + (\sage {p1CNMf3}) + (\sage {p1CNMf4}) + (\sage {p1CNMf5})$. If we know one of the roots is a non-real complex number, what is the best we can say about the number of non-real roots that $p(x)$ has?

Simplify the following expression fully: $$\frac {\sage {p1CNHc7}}{(\sage {p1CNHc8})(\sage {p1CNHc9})}$$

Simplify the following expression fully: $$\frac {\sage {p2CNHc7}}{(\sage {p2CNHc8})\overline {(\sage {p2CNHc9})}}$$

Consider the polynomial $p(x) = \sage {p1PDHf4}$. What is the sum of the zeros of $p(x)$? Hint: $\sage {p1PDHcA}$ is a zero of $p(x)$.

Consider the polynomial $p(x) = \sage {p2PDHf4}$. What is the sum of the zeros of $p(x)$? Hint: $\sage {x - p1PDHcA}$ is a factor of $p(x)$.

When using polynomial long division, if the remainder is zero, what does this mean?

What degree factor can be used as a divisor with polynomial long division?

What is the remainder when $\sage {p1PDMf7}$ is divided by $\sage {p1PDMf6}$?

What method is best for factoring out a complex-valued non-real zero of a polynomial?

Consider the polynomial $p(x) = \sage {p1RRTMf1(x)}$. According to the rational root test, which of the following is NOT a possible zero of $p(x)$?

Consider the polynomial $p(x) = \sage {p1RRTMf1(x)}$. Which of the following can not be a root of the polynomial?

Consider the polynomial $p(x) = \sage {p1RRTHf1}$. Which of the following are true?

I:

$p(x)$ is degree 4.

II:

$p(x)$ has 4 real zeros.

III:

The sum of the zeros of $p(x)$ is $\sage {p1RRTHc3}$.

IV:

The product of the zeros of $p(x)$ is 0.

Can the Rational Root theorem be used to find zeros of a polynomial that has (some) complex-valued zeros?

If you have tried every number listed by rational root theorem and found no roots (and made no mistakes), what does that tell you about the polynomial?

What is the minimal degree polynomial one could use the rational root theorem on?

Which of the following is a zero of the polynomial $p(x) = \sage {p1SDHf5}$?

Which of the following is a factor of the polynomial $p(x) = \sage {p2SDHf5}$?

Which of the following is a zero of the polynomial $p(x) = \sage {p1SDMf5}$?

Which of the following is a factor of the polynomial $p(x) = \sage {p2SDMf5}$?

Can you use Synthetic Division to divide the polynomial $p(x) = \sage {p1SDEf1}$ by $d(x) = \sage {p1SDEdiv}$?

Which of the following is a proper factorization of the polynomial $p(x) = \sage {p1CMEf3}$ (using real coefficients):

When factoring using the coefficient method the original polynomial must...

Which of the following is a proper factorization (using real coefficients) of the polynomial $$p(x) = \sage {p1ACMMf3}$$

When using the AC-method, we are really...

Which of the following is a proper factorization (using real coefficients) of the polynomial $$p(x) = \sage {p1ACMHf3}$$

Which of the following is a proper factorization (using real coefficients) of the polynomial $$p(x) = \sage {p2ACMHf5}$$

Which of the following is a proper factorization (using real coefficients) of the polynomial $$p(x) = \sage {p1ACMEf3}$$

The AC method can be used on...

Which of the following is a proper factorization of the polynomial $p(x) = \sage {p1CMHf3}$ (using real coefficients):

Consider the polynomial $p(x) = \sage {p2CMHf1}$. What is the sum of the zeros of $p(x)$ after is has been shifted to the right by $\sage {p2CMHc3}$?

What number would you add and subtract to the polynomial $p(x) = \sage {p1CtSEf1}$ in order to complete the square?

When using the technique of Completing the Square, you will end up with...

Which of the following is a proper factorization of the polynomial $p(x) = \sage {p1CMMf3}$ (using real coefficients):

Consider the polynomial $f(x) = \sage {p2CMMf1}$. Which of the following statements are true?

I:

$f(x)$ has 2 roots but no real zeros.

II:

$f(x)$ has 2 roots and 2 real zeros.

III:

$f(x)$ is degree 2 which is why it must have 2 real zeros.

IV:

$f(x)$ is degree 2 but has no real zeros.

Complete the square on the expression $$\sage {p1CtSHf1}$$ to get it into the form $A(x+B)^2 + C$. Which of the following is correct:

Consider the polynomial $p(x) = \sage {p1CtSMf1} + C$. What would the value of $C$ need to be in order for $p(x)$ to be a perfect square? (Hint: Try to complete the square and see what number you must add and subtract)

Complete the square on the following quadratic form. (Note: You do not need to fully factor, just complete the square.) $$\sage {p2CtSMf1}$$

Which of the following is a proper factorization of the polynomial $p(x) = \sage {p1GMEf3}$ (using real coefficients):

When factoring by grouping, you need to ensure that...

Which of the following is a proper full factorization (using real coefficients) of the polynomial: $$p(x) = \sage {p1GMHf3}$$

Which of the following is a proper full factorization (using real coefficients) of the polynomial: $$p(x) = \sage {p2GMHf3}$$ Hint: Use factor by grouping.

Which of the following is a proper full factorization of the polynomial $p(x) = \sage {p1GMMf3}$ (using real coefficients):

Consider the polynomial $p(x) = \sage {p2GMMf1}$. What is the sum of the zeros of $p(x)$?

Which of the following is a proper factorization of the polynomial $p(x) = \sage {p1SFEf1}$ (using real coefficients):

Which of the following is not a special form for factoring polynomials with real coefficients?

Which of the following is a proper factorization of the polynomial $p(x) = \sage {p1SFHf1}$ (using real coefficients):

Factor the polynomial $p(x) = \sage {p2SFHf3}$ using real coefficients.

Which of the following is a proper factorization of the polynomial $p(x) = \sage {p1SFMf1}$ (using real coefficients):

Factor the polynomial $p(x) = \sage {p2SFMf3}$ using real coefficients.

Given a polynomial of degree $\sage {p1EEpwr1}$ what can be said about the absolute extrema it has?

Given a polynomial of degree $\sage {p1EEpwr1+1}$ what can be said about the absolute extrema it has?

Given a polynomial with leading term $\sage {p1EHf1}$ what can be said about the number of absolute and relative extrema it has?

Given a polynomial with leading term $\sage {p1EHf2}$ what can be said about the number of absolute and relative extrema it has?

Consider the monomial $p(x) = \sage {p1CEf1}$. Does $p(x)$ have any absolute extrema, if so which type?

Consider the monomial $p(x) = \sage {p2CEf1}$. Is $p(x)$ increasing, or decreasing to the right of the origin?

Given a polynomial with leading term $\sage {p1EMf1}$ what can be said about the absolute extrema it has?

Given a polynomial with leading term $\sage {p1EMf2}$ what can be said about the absolute extrema it has?

Consider the following graph:

Based on the number of extrema, what is the smallest degree possible for the leading term of $f$?

Consider the following graph:

Within which of the following segments is the function increasing and concave down?

What is the leading coefficient of $(\sage {p1idFTAEf1}) + (\sage {p1idFTAEf2}) + (\sage {p1idFTAEf3}) + (\sage {p1idFTAEf4}) + (\sage {p1idFTAEf5})$?

Which of the following equations are polynomials?

(a)

$f(x) = x^2 + 1$

(b)

$g(x) = \frac {1}{3}x^3 + 7$

(c)

$h(x) = 7$

(d)

$k(x) =x^3 + 3x^{\frac {1}{3}} + 1$

Which of the following is the graph of $f(x) = (-x+2)^3 - 1$?

 Correct

 Try again

 Check work

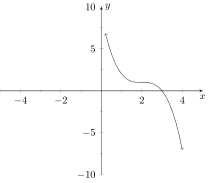
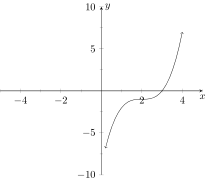
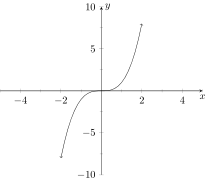
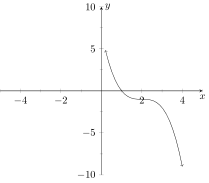
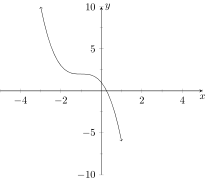
Consider the polynomial $p(x) = \sage {p1idFTAMf4}$. How many zeros does this polynomial have counting multiplicity?

How many zeros (and what type) does the polynomial $\sage {p2idFTAMf1}$ have?